Potentials with the Potential to Be Real

Many of us have heard that its bad to charge our devices with chargers that deliver higher voltages than what they’re rated for. We know that voltage refers to electrical potential difference, but what actually is electrical potential physically? Its units, energy per unit charge, guide our intuition, yet it often feels like a bookkeeping tool rather than something observable.

Electrostatic fields produced by point charges are conservative, meaning their fields can be written as the gradient of a scalar potential V as shown in Equation 1 (Villamizar 2025).

However, magnetic fields are more difficult because they usually appear due to the movement of charged particles. There is no scalar function whose gradient produces the magnetic field (Semon and Taylor 1996). However, you can express the magnetic field as the curl of some potential vector function (A) instead (Equation 2).

Unlike electric potential, the magnetic vector potential has had a blurry physical interpretation and was often regarded a mathematical tool that can simplify calculations (Vaidman 2012). However, this would soon change as the field of quantum mechanics began to emerge.

In 1926, Erwin Schrödinger published his wave equation; a differential equation that describes how the quantum state of a system evolves through time (Schrödinger 1926). The one-dimensional version is displayed in Equation 3, where V represents the electrostatic potential, m is the mass of the particle, and ℏ is a constant.

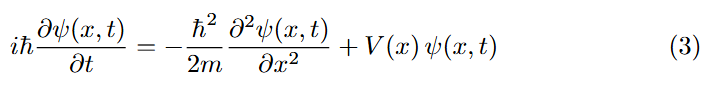
The solution to this equation is the wavefunction denoted by (Ψ). While the wavefunction on its own doesn’t yield any information physically observable, taking the modulus squared gives you the probability density which tells you how likely you are to find the particle at position (x) and time (t) (Born 1926). In the case of a spatially unbounded, charged particle in electromagnetic potentials, the wavefunction takes the form as shown in Equation 4,

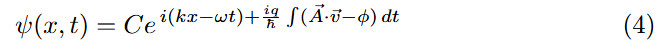
where C is a constant and the terms in the exponents control the phase of the wavefunction. Observe that the magnetic vector potential makes an appearance here. This suggests that this “mathematical tool” would create real observable effect right?

This was precisely the insight of David Bohm and Yakir Aharonov in 1959. They proposed that electrons traveling in a region with no magnetic field could still exhibit a shift in their interference pattern if a magnetic vector potential were present (Aharonov and Bohm 1959). The striking implication was that a particle could be influenced by electromagnetic potentials even when it never directly encounters a magnetic field. This prediction became known as the Aharonov-Bohm (AB) effect.

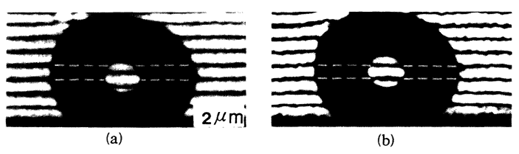
Nearly 20 years after its proposal, a team of scientists led by Akira Tonomura experimentally verified the AB effect in 1986 (Tonomura 1986). They fabricated a microscopic toroidal magnet entirely embedded in superconducting niobium to contain the magnetic field inside of the magnet. Then they fired an electron beam at the magnet; a beam was wide enough to be treated as two relative to the magnet. One of the beams served as a control and passed through free space while the other beam entirely washed over the magnet. Then the electron beams were deflected towards each other, causing them to intersect and creating the interferences patterns observed in Figure 1. Due to the geometry of the magnet, the magnetic vector potential is different outside the magnet than at the center.

The Aharonov-Bohm effect blurs the lines between what is truly physical and mathematical. What started off as a merely a calculational tool ended up having physical meaning on a scale that was simply not explored at the time of its creation. As of right now, quantum mechanics is still relatively young with many more unsolved mysteries. It makes you wonder many more “mathematical tools” still exist in the formulation of physics that have undiscovered meaning?

References

Aharonov, Y., and D. Bohm. 1959. “Significance of Electromagnetic Potentials in the Quantum Theory.” Physical Review 115 (3): 485–91. https://doi.org/10.1103/PhysRev.115.485.

Born, Max. 1926. “Zur Quantenmechanik der Stoßvorgänge.” Zeitschrift für Physik 37 (12): 863–67. https://doi.org/10.1007/BF01397477.

Schrödinger, E. 1926. “Quantisierung Als Eigenwertproblem.” Annalen Der Physik 384 (4): 361–76. https://doi.org/10.1002/andp.19263840404.

Semon, Mark D., and John R. Taylor. 1996. “Thoughts on the Magnetic Vector Potential.” American Journal of Physics 64 (11): 1361–69. https://doi.org/10.1119/1.18400.

Tonomura, Akira, Nobuyuki Osakabe, Tsuyoshi Matsuda, et al. 1986. “Evidence for Aharonov-Bohm Effect with Magnetic Field Completely Shielded from Electron Wave.” Physical Review Letters 56 (8): 792–95. https://doi.org/10.1103/PhysRevLett.56.792.

Vaidman, Lev. 2012. “Role of Potentials in the Aharonov-Bohm Effect.” Physical Review A 86 (4): 040101. https://doi.org/10.1103/PhysRevA.86.040101.

Villamizar, David Velasco. 2025. “A Didactical Approach to Teaching Electric Field and Electric Potential Concepts.” Revista Brasileira de Ensino de Física 47: e20250334. https://doi.org/10.1590/1806-9126-RBEF-2025-0334.