The beauty of mathematics is in the complexity that arises from simple rules. Take the following sequence of numbers: {1, 1, 2, 3, 5, 8, 13, 21, …}. To get this sequence, start with the number 1, add 0 and you get the next number in the sequence: 1. Take 1 and add the previous number to get 2. Add that number to the number preceding it and get the next element of the sequence, continuing this pattern results in a set of numbers known as the Fibonacci sequence. Now take the second number and divide it by the first number (1/1=1). Do this with every pair of successive numbers until infinity (or at least for a very long time if you are too busy to go to infinity) and you will find that each ratio of successive numbers in the sequence converges to one strangely irrational number: 1.61803…. This number is known as Φ, the Golden Ratio. There are many interesting properties of this ratio that give rise to what some might say spooky applications in the real world. These uncanny recurrences inspire people to appreciate the true connection between abstract mathematics and reality.
Figure 1: The succession of leaf growth position (Richter, 1978).
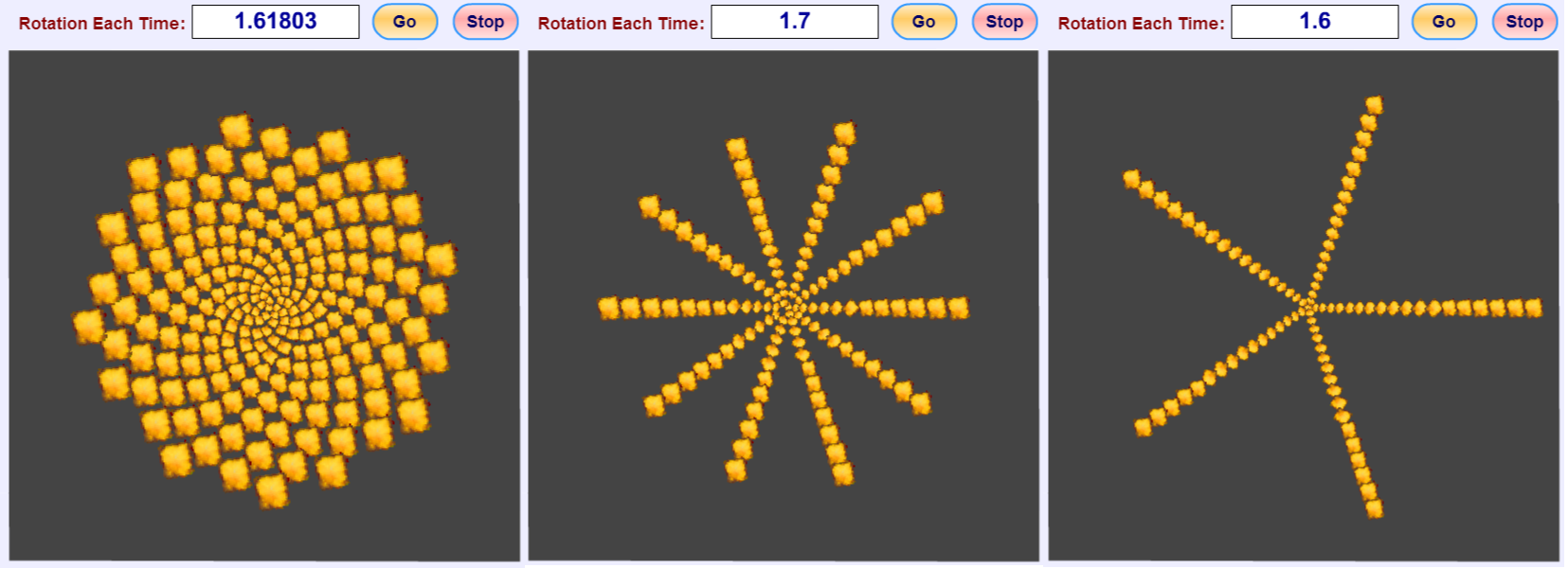
Leaves grow around plant stems in angles that are Φ-th of a rotation (360/Φ degrees, also known as the Golden Angle) away from preceding leaves. Richter suggests that these spirals emerge due to the fact that new leaves secrete inhibitory responses to signal newer leaves not to grow above that leaf (Richter, 1978). Newer leaves that follow will be repelled by both the first and second leaves and what results is a pattern of leaf growth in which the angle of successive leaves is the Golden Angle (Figure 1). Overall, a spiral pattern emerges such that an overall area is fully covered. If the leaves did not grow in such a pattern, there would be inefficient gaps in the spiral, as shown in Figure 2. As a result, a greater area is covered by leaves while they are not overlapping, thus optimizing photosynthetic potential.
Figure 2: Created with an interactive animation from MathIsFun.com showing the patterns that arise as leaves grow at various angles. It is clear that if leaves are added every Φ-th of a rotation, then an optimal surface area for photosynthesis is achieved (MathIsFun.com, 2014).
Figure 3: On the left is a relatively healthy heart and on the right is a heart from a patient with severe heart failure. The vertical and transverse dimensions are drawn in yellow and red, respectively (Henein, 2011).
Another recurrence of the Golden Ratio is in the human body. Published in the International Journal of Cardiology, Henein reveals that in healthy individuals the ratio between the vertical and transverse lengths of the heart chambers correspond to Φ, while those with end-stage heart failure do not (Henein, 2011). As shown in Figure 3, the ratio between the yellow and red lengths resemble the Golden Ratio and this ratio deteriorates as the health of the heart suffers. Although this may seem like a mere coincidence, Henein continues to suggest that having these dimensions of the heart give the organ optimal pump structure and function efficiency.
Figure 4: A Euclidean-construction of a Fibonacci rectangle. The relationship between proper and improper time can be clearly visualized in this diagram (Sigalotti, 2006).
Not only does the Golden Ratio appear in biology, but this mathematical phenomenon has its applications in the pedagogy of physics. Φ can be cleverly used to provide an accessible and intuitive way to derive the equations for the dilation of time intervals and length contraction (Sigalotti, 2006). Figure 4 shows a Euclidean-constructed rectangle in which the length BE (E being the midpoint between A and C) is equal to the length EF. This results in a rectangle CFGD, where CF/FG is the Golden Ratio. Furthermore, the dimensions of rectangle AFGB exhibit the same ratio. In other words, CD/CF= AB/AF = Φ. Using these two rectangles, we can clearly see a relationship between improper time (Δt), the time observed at an inertial frame of reference and proper time (Δt’), the time observed by an object moving at relativistic speeds. From this careful construction of side-lengths, Sigalotti was able to derive Einstein’s exact equation of time dilation. This particular construction can be used in the classroom to give students an intuition of how time changes at relativistic speeds. At lower speeds, the square collapses and the improper time becomes more similar to proper time, which explains why significant time dilation effects are not experienced on Earth.
These are only a few accounts in which the Golden Ratio appears in the natural sciences. In addition to scientific applications, this ratio is known historically to be an aesthetically pleasing proportion. As such, this ratio appears as the proportions for ancient Greek and Roman architecture and even in art pieces by Leonardo da Vinci. The Golden Ratio is truly a testament to how mathematical constructs can be evident in the real world.
References
Henein, M. Y. (2011). The human heart: Application of the golden ratio and angle. International Journal of Cardiology, 150(3), 239 – 242. doi: 10.1016/j.ijcard.2011.05.094
MathIsFun.com. (2014). Nature, The Golden Ratio, and Fibonacci too. Retrieved from: https://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html. Accessed: November 14, 2015.
Richter, P. (1978). Leaf arrangement. Naturwissenschaften, 65(6), 319 – 327. doi: 10.1007/BF00368372
Sigalotti, L. D. G. (2006). The golden ratio in special relativity. Chaos, Solitons and Fractals, 30(3), 521 – 524. doi: 10.1016/j.chaos.2006.03.005