As early as toddlerhood, our brains have been ingrained with the fundamental principle that one plus one equals two. This notion: that when you add two things together, you achieve a sum that is larger than either of the two original inputs, is near common sense. However, as in all sectors science, there are exceptions to the rules, and in this case that exception is mass defect (MD). MD is the difference in the actual mass of an atomic nuclei, and the predicted mass that is based on the constituent of protons and neutrons (Equation 1) (Pourshahian 2017).

Equation 1. MD equation, where delta m is the difference in mass between the constituents and the measured mass of a nucleus. Z is the atomic number, mp is the mass of a proton: 1.672 x 10-27kg, A is the mass number, mn is the mass of a neutron 1.674 x 10-27kg, and mnuc is the recorded measured mass of the nucleus of interest.
In the case of a Helium atom that has 2 protons, a mass number of 4, and recorded mass of 6.646 x 10-27 kg, the MD of the nucleus is given by: (Equation 2).

Equation 2. The calculated MD of a helium nucleus in kilograms. Note: electrons mass are negligible in comparison and thus not included in calculations.
This can be a confusing concept at first: how can something have less mass than the sum of its constituents? The answer… energy (Kneubil 2018)! During the formation of a nucleus in its exothermic reaction, some of the mass that makes up the constituents was lost in order to form the atoms nucleus. This is explained by Einstein’s famous “mass-energy equivalence” formula that states that mass and energy can be converted between one another by a constant (the speed of light squared) (Equation 3) (Borchardt 2015). Not only does this equation relate mass to energy, but it is also used to determine the amount of energy required to break apart a nucleus into its constituents once again.

Equation 3. Einstein’s mass energy equivalence equation that converts mass into energy.
This amount of energy is known as the nuclear binding energy (Coc 2011). A useful application of nuclear binding energy is determining the binding energy per nucleon (BEN). The BEN (Equation 4) is analogous to the ionization energy of an atom and plays a crucial role in nuclear physics; if the BEN is high, it tells us that the nucleus is relatively stable. A stable nucleus does not decay spontaneously or emit any kind of radioactivity.

Equation 4. A calculation of the BEN of a nucleon, which is the average energy that is required to remove an individual nucleon from a nucleus. Where E is the energy that was derived by equation 3, and A is the is the mass number of the nucleus of interest.
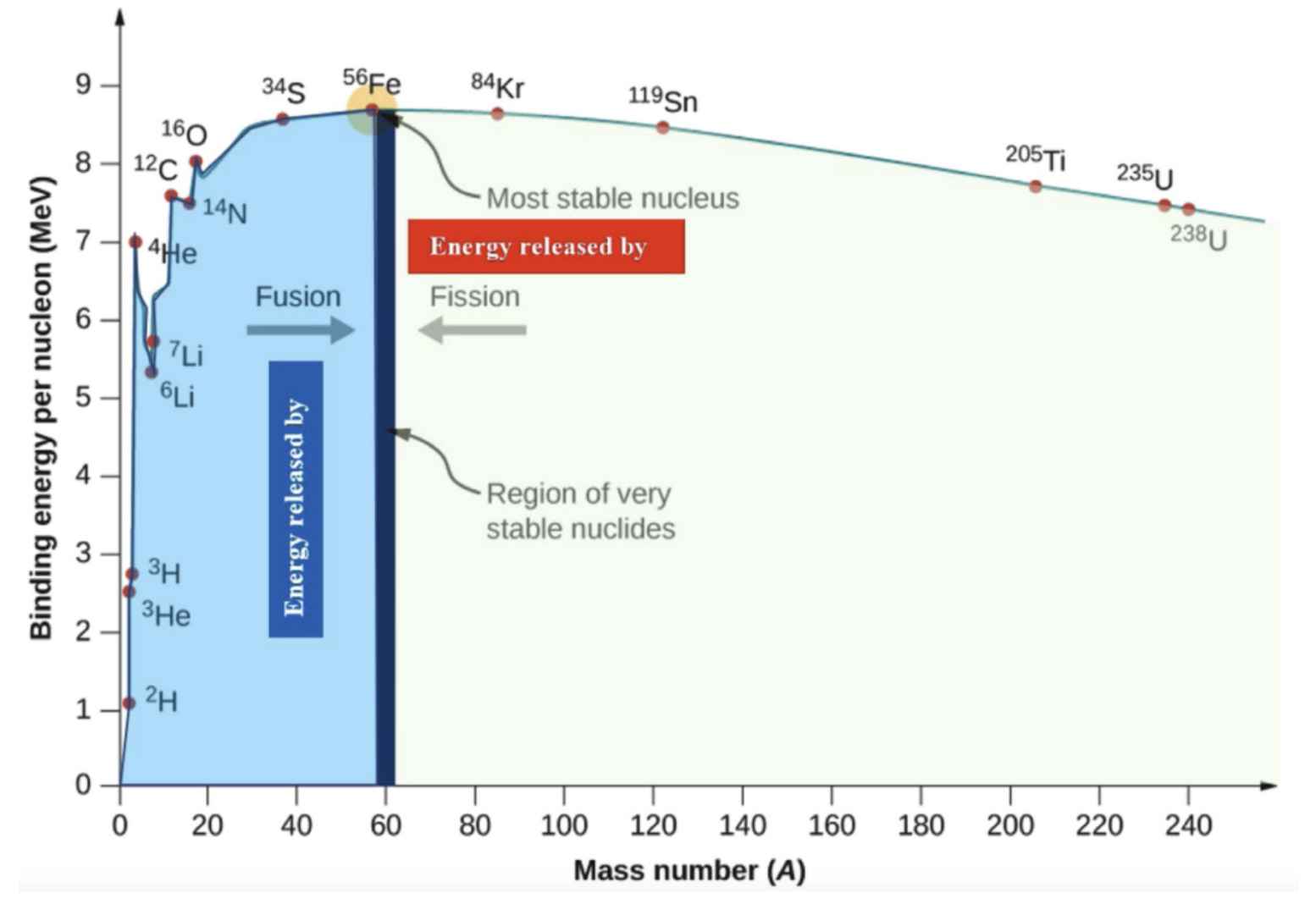
A Typical BEN range is from 6-10 MeV, this is why the nuclear force is known as the strong force as it takes several million electron volts to remove a nucleon from a nucleus (Blake 2011). Different elements have a variety of BEN that generally increases as you go further down the periodic table (Figure 1).

Figure 1. The binding energy per nucleon vs the mass number. The greatest BEN occurs at 56Fe meaning that it is an extremely stable isotope (Paraschiv, Paraschiv, and Dragan 2022).
MD has extremely important implications in the nuclear world as it is a building block for many subatomic interactions including binding energy, and subsequently BEN. So next time you see 1 + 1 consider… does it really equal 2?
References
Blake, Russ. 2011. “The Architecture of Nuclear Binding Energy.” Physics Procedia, 2011 International Conference on Physics Science and Technology (ICPST 2011), 22 (January):40–55. https://doi.org/10.1016/j.phpro.2011.11.007.
Borchardt, Glenn. 2015. “The Physical Meaning of E=mc2.” In . Vol. 6. https://doi.org/10.13140/RG.2.1.2387.4643.
Coc, Alain. 2011. “Nuclear Stability.” In Encyclopedia of Astrobiology, edited by Muriel Gargaud, Ricardo Amils, José Cernicharo Quintanilla, Henderson James (Jim) Cleaves, William M. Irvine, Daniele L. Pinti, and Michel Viso, 1135–1135. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-642-11274-4_1076.
Kneubil, Fabiana B. 2018. “E = Mc2 and the Weight of Energy.” European Journal of Physics 40 (1): 015604. https://doi.org/10.1088/1361-6404/aae7a6.
Paraschiv, Lizica Simona, Spiru Paraschiv, and Marcel Dragan. 2022. “A Web Application to Calculate the Mass Defect and Nuclear Binding Energy per Nucleon.” Energy Reports, Technologies and Materials for Renewable Energy, Environment and Sustainability, 8 (November):342–50. https://doi.org/10.1016/j.egyr.2022.06.087.
Pourshahian, Soheil. 2017. “Mass Defect from Nuclear Physics to Mass Spectral Analysis.” Journal of The American Society for Mass Spectrometry 28 (9): 1836–43. https://doi.org/10.1007/s13361-017-1741-9.